Calculo Integral: Unidad 4 Series

4.7 Cálculo de Integrales de funciones
expresadas como serie de Taylor.

En el calculo se le da una gran valor al matemático británico Brook Taylor, quien lo enunció el teorema de Taylor con mayor generalidad en 1712.

Este teorema permite obtener aproximaciones polinómicas de una función en un entorno de cierto punto en que la función sea diferenciable. Además el teorema permite acotar el error obtenido mediante dicha estimación.

Teorema:

Si n ≥ 0 es un entero y f una función que es derivable n veces en el intervalo cerrado [a,x] y n+1 veces en el intervalo abierto (a,x), entonces se cumple que:

$f\left( x \right) = \sum\limits_{k = 0}^n {\frac{{f^{\left( k \right)} (a)}}{{k!}}} (x - a)^k + R_n (f)$

Donde $R_n (f)$ denota el resto de de aproximar f por el polinomio depende de x y es pequeño si x está próximo al punto a.

$R_n (f) = \frac{{f^{\left( {n + 1} \right)} \left( \xi \right)}}{{\left( {n + 1} \right)!}}\left( {x - a}\right)^{n + 1}$ y $\xi$ es un número entre a y x.

En general si la (n+1) derivada de f está acotada por una constante M en el intervalo (a,b) que se menciona en el teorema de Taylor, es decir, si

$\left| {f^{\left( {n + 1} \right)} \left( x \right)} \right| \leqslant M$ para todo x en (a,b)

entonces 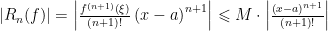$\left| {R_n (f)} \right| = \left| {\frac{{f^{\left( {n + 1} \right)}\left( \xi \right)}}{{\left( {n + 1} \right)!}}\left( {x - a} \right)^{n + 1} } \right| \leqslant M \cdot \left|{\frac{{\left( {x - a} \right)^{n + 1} }}{{\left( {n + 1} \right)!}}} \right|$

Cuando n crece indefinidamente entonces 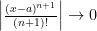$\left| {\frac{{\left( {x - a} \right)^{n + 1} }}{{(n + 1)!}}} \right| \to 0$

Ejemplo:

Ejemplo 1. Encuentre el polinomio de grado 4 que satisface:

P(2) = 3, P '(2) = 5, P ⁽²⁾(2) = 4, P ⁽³⁾(2) =24 y P ⁽⁴⁾(2) =48

Solución: Para encontrar la expresión del polinomio en términos de (x-2), simplemente sustituimos x_o = 2 y n = 4 en la expresión ( I ), obteniendo:

y por lo tanto el polinomio buscado es:

P(x) = 3 + 5(x-2) + 2(x-2)² + 4(x - 2)³ + 2(x - 2)⁴

Referencia Bibliografica:

http://es.wikipedia.org/wiki/Teorema_de_Taylor
http://www.mat.uson.mx/eduardo/calculo2/soltaylor/soltaylorHTML/taylor.htm
http://www.aulademate.com/blog/taylor/

Calculo Integral

Vistas de página en total

jueves, 19 de mayo de 2011

Unidad 4 Series

1 comentario: